7. Financial time series

Python and, in particular, pandas can easily deal with the most common type of financial data - time series data. We are going to look at the basics of using price and return data. This section follows Chapter 8 of Python for Finance, 2e and the fourth DataCamp assignment that discusses pandas time series.

We’ll cover importing time series data and getting some summary statistics, as well as return calculations, resampling, or changing the periodicity of the data (i.e. going from daily to monthly to annual), and rolling statistics, such as finding moving averages and other statistics over rolling windows (e.g. one month of trading days).

Time series data means handling dates. There is a DataCamp tutorial on datetime objects.

We’ll start with the usual sort of set-up and our familiar stock data. Our data is going to have a particular set-up in this section. Each column is going to represent both a security and something about that security. So, Apple’s price. Or, Apple’s return. This is a very common way to see financial data, but it is not the only way that this data can be organized.

7.1. Set-up and descriptives

# Set-up

import numpy as np
import pandas as pd

# Date functionality
from datetime import datetime
from datetime import timedelta

import janitor
from janitor import clean_names

# all of matplotlib
import matplotlib as mpl 

# refer to the pyplot part of matplot lib more easily. Just use plt!
import matplotlib.pyplot as plt

# importing the style package
from matplotlib import style
from matplotlib.ticker import StrMethodFormatter

# generating random numbers
from numpy.random import normal, seed
from scipy.stats import norm

# seaborn
import seaborn as sns

# Keeps warnings from cluttering up our notebook. 
import warnings
warnings.filterwarnings('ignore')

# Include this to have plots show up in your Jupyter notebook.
%matplotlib inline 

# Some plot options that will apply to the whole workbook
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'


# Read in some eod prices
stocks = pd.read_csv('https://raw.githubusercontent.com/aaiken1/fin-data-analysis-python/main/data/tr_eikon_eod_data.csv',
                  index_col=0, parse_dates=True)  

stocks.dropna(inplace=True)  

stocks = clean_names(stocks)

stocks.info()

/opt/anaconda3/lib/python3.9/site-packages/seaborn/rcmod.py:82: DeprecationWarning: distutils Version classes are deprecated. Use packaging.version instead.
  if LooseVersion(mpl.__version__) >= "3.0":
/opt/anaconda3/lib/python3.9/site-packages/setuptools/_distutils/version.py:346: DeprecationWarning: distutils Version classes are deprecated. Use packaging.version instead.
  other = LooseVersion(other)

<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 2138 entries, 2010-01-04 to 2018-06-29
Data columns (total 12 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   aapl_o  2138 non-null   float64
 1   msft_o  2138 non-null   float64
 2   intc_o  2138 non-null   float64
 3   amzn_o  2138 non-null   float64
 4   gs_n    2138 non-null   float64
 5   spy     2138 non-null   float64
 6   _spx    2138 non-null   float64
 7   _vix    2138 non-null   float64
 8   eur=    2138 non-null   float64
 9   xau=    2138 non-null   float64
 10  gdx     2138 non-null   float64
 11  gld     2138 non-null   float64
dtypes: float64(12)
memory usage: 217.1 KB

We are using pandas DataFrames, which have many built-in ways to deal with time series data. We have made our index the date. This is important - having the date be our index opens up various date-related methods.

Let’s use pandas plot to make a quick figure of all of the prices over the time period in our data. Remember, pandas has its own plotting functions. They are very useful for quick plots like this. Because the date is our index, pandas knows to put that on the x-axis, right where we want it.

stocks.plot(figsize=(10, 12), subplots=True);  

No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.

No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.

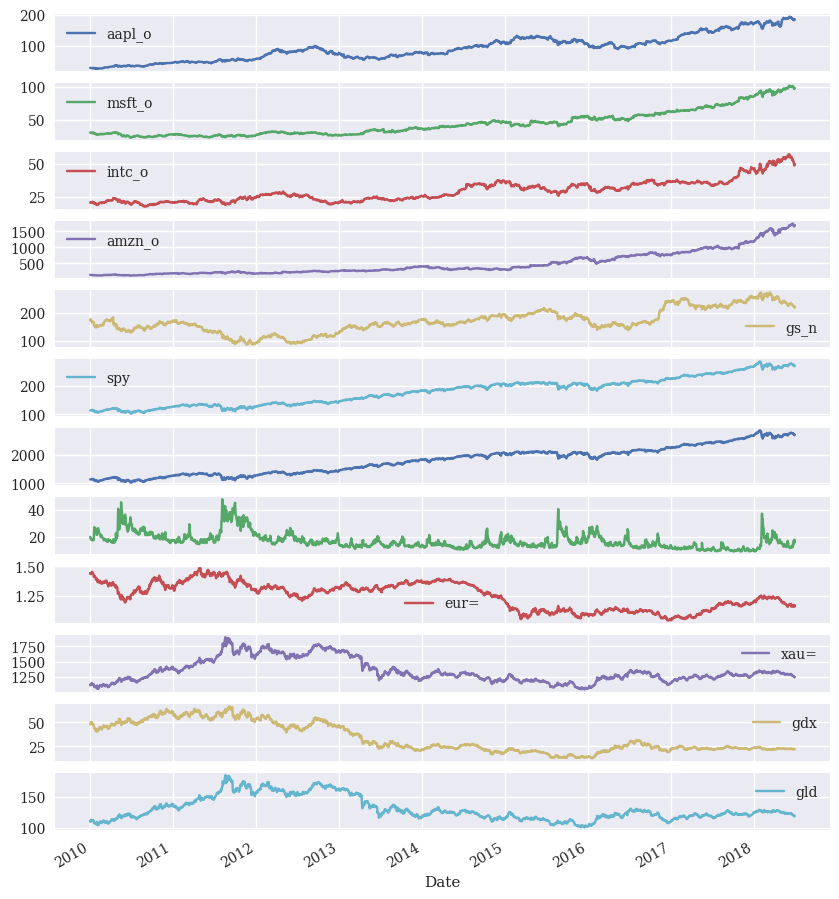
We can use .describe() to look at our prices.

stocks.describe().round(2) 

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
count	2138.00	2138.00	2138.00	2138.00	2138.00	2138.00	2138.00	2138.00	2138.00	2138.00	2138.00	2138.00
mean	93.46	44.56	29.36	480.46	170.22	180.32	1802.71	17.03	1.25	1348.91	33.57	130.09
std	40.55	19.53	8.17	372.31	42.48	48.19	483.34	5.88	0.11	188.21	15.17	18.78
min	27.44	23.01	17.66	108.61	87.70	102.20	1022.58	9.14	1.04	1051.36	12.47	100.50
25%	60.29	28.57	22.51	213.60	146.61	133.99	1338.57	13.07	1.13	1222.49	22.14	117.40
50%	90.55	39.66	27.33	322.06	164.43	186.32	1863.08	15.58	1.27	1292.68	25.62	124.00
75%	117.24	54.37	34.71	698.85	192.13	210.99	2108.94	19.07	1.35	1427.57	48.34	139.00
max	193.98	102.49	57.08	1750.08	273.38	286.58	2872.87	48.00	1.48	1897.10	66.63	184.59

We can use .aggregate() to create our own set of descriptives.

stocks.aggregate([min,  
                np.mean,  
                np.std,  
                np.median,  
                max]  
).round(2)

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
min	27.44	23.01	17.66	108.61	87.70	102.20	1022.58	9.14	1.04	1051.36	12.47	100.50
mean	93.46	44.56	29.36	480.46	170.22	180.32	1802.71	17.03	1.25	1348.91	33.57	130.09
std	40.55	19.53	8.17	372.31	42.48	48.19	483.34	5.88	0.11	188.21	15.17	18.78
median	90.55	39.66	27.33	322.06	164.43	186.32	1863.08	15.58	1.27	1292.68	25.62	124.00
max	193.98	102.49	57.08	1750.08	273.38	286.58	2872.87	48.00	1.48	1897.10	66.63	184.59

7.1.1. Dates

The fourth Datacamp assignment covers some additional date basics. Two libraries are being used here: datetime and pandas. We can use pandas to objects and methods that help us deal with dates. Obviously, we need to handle a variety of time periods in finance.

We can define a TimeStamp and see that they are a particular object-type in Python. All objects come with methods and attributes. This is a generic idea from computer science called object oriented programming.

my_date = pd.Timestamp(datetime(2022, 2, 23))
print(type(my_date))
my_date

<class 'pandas._libs.tslibs.timestamps.Timestamp'>

Timestamp('2022-02-23 00:00:00')

Here’s an example of an attribute for a TimeStamp object. You can also do .month, .day, .dayofweek, etc.

my_date.year

2022

We can add and subtract with dates using timedelta. Note that datetime no longer wants you to just add or subtract a number from a date.

There’s both a datetime timedelta and a pandas Timedelta. You can read about the pandas version here.

my_date + timedelta(days=7)

Timestamp('2022-03-02 00:00:00')

Using the pandas version, just to highlight that different libraries have similar functionality. The datetime library and the pandas library are different things. But, they can do similar operations with time, even if the syntax varies a bit.

my_date + pd.Timedelta(7, "d")

Timestamp('2022-03-02 00:00:00')

pandas has a set of tools related to a period in time. You can define a period, get attributes, and change its frequency. Changing the frequency means changing how pandas thinks about the period. Is this month? Is this a particular day?

Let’s define a period as February 2022.

period = pd.Period('2022-02')
period

Period('2022-02', 'M')

We can then change that to a daily frequency. Note how, by default, pandas puts us at the end of the month.

period.asfreq('D')

Period('2022-02-28', 'D')

This can be really helpful when some Excel data comes in as, say “May-2019” and we want to get that to be an end of month date, like “5/31/19”. The actual day is ambiguous when just dealing with month and year.

With the date as our index, we can pull certain dates and columns. Here’s Apple’s price on 2017-6-1.

stocks.loc['2017-6-1', 'aapl_o']

153.18

Here’s all of the columns, but just for a subset of dates.

stocks.loc['2015-3':'2016-2',:]

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2015-03-02	129.09	43.880	34.060	385.655	191.79	211.9900	2117.39	13.04	1.1183	1206.70	20.76	115.68
2015-03-03	129.36	43.280	34.095	384.610	191.27	211.1200	2107.78	13.86	1.1174	1203.31	20.38	115.47
2015-03-04	128.54	43.055	34.120	382.720	189.67	210.2301	2098.53	14.23	1.1077	1199.45	20.04	115.11
2015-03-05	126.41	43.110	33.730	387.830	190.08	210.4600	2101.04	14.04	1.1028	1198.20	20.08	115.00
2015-03-06	126.60	42.360	33.190	380.090	186.91	207.5000	2071.26	15.20	1.0843	1166.72	18.58	111.86
...	...	...	...	...	...	...	...	...	...	...	...	...
2016-02-23	94.69	51.180	28.800	552.940	144.91	192.3200	1921.27	20.98	1.1017	1227.06	18.92	117.22
2016-02-24	96.10	51.360	29.190	554.040	145.56	193.2000	1929.80	20.72	1.1011	1228.96	19.11	117.61
2016-02-25	96.76	52.100	29.620	555.150	148.25	195.5400	1951.70	19.11	1.1021	1234.26	19.39	117.92
2016-02-26	96.91	51.300	29.800	555.230	150.25	195.0892	1948.05	19.81	1.0931	1222.21	18.69	117.11
2016-02-29	96.69	50.880	29.590	552.520	149.53	193.5600	1932.23	20.55	1.0871	1237.76	19.38	118.64

252 rows × 12 columns

7.2. Calculating returns

We can start by just calculating the price change from day-to-day using pandas diff(). This function is described here. Notice how the first day in the data is now NaN, since you can’t calculate a change without the previous day.

Since there’s no =, I am not saving the data. Just showing you what the function does.

stocks.diff().head() 

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2010-01-04	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2010-01-05	0.052857	0.010	-0.01	0.79	3.06	0.30	3.53	-0.69	-0.0043	-1.35	0.46	-0.10
2010-01-06	-0.487142	-0.190	-0.07	-2.44	-1.88	0.08	0.62	-0.19	0.0044	19.85	1.17	1.81
2010-01-07	-0.055714	-0.318	-0.20	-2.25	3.41	0.48	4.55	-0.10	-0.0094	-6.60	-0.24	-0.69
2010-01-08	0.200000	0.208	0.23	3.52	-3.36	0.38	3.29	-0.93	0.0094	4.20	0.74	0.55

Sometimes we want price changes. Other times we want pandas pct_change(). See this for more. This function allows us to calculate price returns using the percent change. The default is to look back one period, or one day in this case.

stocks.pct_change().mul(100).round(3).head()  

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2010-01-04	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2010-01-05	0.173	0.032	-0.048	0.590	1.768	0.265	0.312	-3.443	-0.298	-0.121	0.964	-0.091
2010-01-06	-1.591	-0.614	-0.335	-1.812	-1.067	0.070	0.055	-0.982	0.306	1.774	2.429	1.650
2010-01-07	-0.185	-1.033	-0.962	-1.701	1.957	0.422	0.400	-0.522	-0.652	-0.580	-0.486	-0.619
2010-01-08	0.665	0.683	1.117	2.708	-1.891	0.333	0.288	-4.879	0.657	0.371	1.507	0.496

I’m multiplying by 100 just for the display of the data.

The percent change is called a linear return. Or, simple return. This is different from log returns, or compounded returns. Both types of returns are correct and useful. They are just used for different things.

The formula for simple returns (R) is:

(7.1)\[\begin{align} R_{t} = \frac{V_t}{V_{t-1}} - 1 \end{align}\]

where R is the simple return based on the percent change and V is the cash flow, including price and dividends (if any).

The formula for log returns (r) is:

(7.2)\[\begin{align} r_{t} = ln(\frac{V_t}{V_{t-1}}) = ln(1 + R_{t}) \end{align}\]

See this article for more on why this difference is important. In short, we need the mean of simple returns when doing portfolio optimization, as these returns work with a weighted average. Simple returns aggregate across assets. Log returns, however, aggregate across time. In other words, the cumulative return using log returns is the sum of individual log returns over the time period. You definitely can’t do that with simple returns!

Here’s a brief video that describes the same thing using Excel.

Finally, this chapter has everything you’ve ever want to know about return calculations. See pgs. 16 and 17 for log returns.

We can calculate log returns using np.log and .shift() from pandas. Let’s look at what .shift() does. Compare the following:

stocks

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2010-01-04	30.572827	30.950	20.88	133.90	173.08	113.33	1132.99	20.04	1.4411	1120.00	47.71	109.80
2010-01-05	30.625684	30.960	20.87	134.69	176.14	113.63	1136.52	19.35	1.4368	1118.65	48.17	109.70
2010-01-06	30.138541	30.770	20.80	132.25	174.26	113.71	1137.14	19.16	1.4412	1138.50	49.34	111.51
2010-01-07	30.082827	30.452	20.60	130.00	177.67	114.19	1141.69	19.06	1.4318	1131.90	49.10	110.82
2010-01-08	30.282827	30.660	20.83	133.52	174.31	114.57	1144.98	18.13	1.4412	1136.10	49.84	111.37
...	...	...	...	...	...	...	...	...	...	...	...	...
2018-06-25	182.170000	98.390	50.71	1663.15	221.54	271.00	2717.07	17.33	1.1702	1265.00	22.01	119.89
2018-06-26	184.430000	99.080	49.67	1691.09	221.58	271.60	2723.06	15.92	1.1645	1258.64	21.95	119.26
2018-06-27	184.160000	97.540	48.76	1660.51	220.18	269.35	2699.63	17.91	1.1552	1251.62	21.81	118.58
2018-06-28	185.500000	98.630	49.25	1701.45	223.42	270.89	2716.31	16.85	1.1567	1247.88	21.93	118.22
2018-06-29	185.110000	98.610	49.71	1699.80	220.57	271.28	2718.37	16.09	1.1683	1252.25	22.31	118.65

2138 rows × 12 columns

stocks.shift(1)

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2010-01-04	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2010-01-05	30.572827	30.950	20.88	133.90	173.08	113.33	1132.99	20.04	1.4411	1120.00	47.71	109.80
2010-01-06	30.625684	30.960	20.87	134.69	176.14	113.63	1136.52	19.35	1.4368	1118.65	48.17	109.70
2010-01-07	30.138541	30.770	20.80	132.25	174.26	113.71	1137.14	19.16	1.4412	1138.50	49.34	111.51
2010-01-08	30.082827	30.452	20.60	130.00	177.67	114.19	1141.69	19.06	1.4318	1131.90	49.10	110.82
...	...	...	...	...	...	...	...	...	...	...	...	...
2018-06-25	184.920000	100.410	52.50	1715.67	226.02	274.74	2754.88	13.77	1.1655	1268.49	22.18	120.34
2018-06-26	182.170000	98.390	50.71	1663.15	221.54	271.00	2717.07	17.33	1.1702	1265.00	22.01	119.89
2018-06-27	184.430000	99.080	49.67	1691.09	221.58	271.60	2723.06	15.92	1.1645	1258.64	21.95	119.26
2018-06-28	184.160000	97.540	48.76	1660.51	220.18	269.35	2699.63	17.91	1.1552	1251.62	21.81	118.58
2018-06-29	185.500000	98.630	49.25	1701.45	223.42	270.89	2716.31	16.85	1.1567	1247.88	21.93	118.22

2138 rows × 12 columns

stocks.shift(1) has moved the previous price up one row. You can do a also do stocks.shift(-1), which pulls prices from the next period to the previous one.

stocks.shift(-1)

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2010-01-04	30.625684	30.960	20.87	134.690	176.14	113.63	1136.52	19.35	1.4368	1118.65	48.17	109.70
2010-01-05	30.138541	30.770	20.80	132.250	174.26	113.71	1137.14	19.16	1.4412	1138.50	49.34	111.51
2010-01-06	30.082827	30.452	20.60	130.000	177.67	114.19	1141.69	19.06	1.4318	1131.90	49.10	110.82
2010-01-07	30.282827	30.660	20.83	133.520	174.31	114.57	1144.98	18.13	1.4412	1136.10	49.84	111.37
2010-01-08	30.015684	30.270	20.95	130.308	171.56	114.73	1146.98	17.55	1.4513	1152.60	50.17	112.85
...	...	...	...	...	...	...	...	...	...	...	...	...
2018-06-25	184.430000	99.080	49.67	1691.090	221.58	271.60	2723.06	15.92	1.1645	1258.64	21.95	119.26
2018-06-26	184.160000	97.540	48.76	1660.510	220.18	269.35	2699.63	17.91	1.1552	1251.62	21.81	118.58
2018-06-27	185.500000	98.630	49.25	1701.450	223.42	270.89	2716.31	16.85	1.1567	1247.88	21.93	118.22
2018-06-28	185.110000	98.610	49.71	1699.800	220.57	271.28	2718.37	16.09	1.1683	1252.25	22.31	118.65
2018-06-29	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN

2138 rows × 12 columns

So, by dividing stocks by stocks.shift(1), we are dividing today’s price by yesterday’s price. Note how we are dividing one DataFrame by another, in a sense. This is an example of vectorization. No need to loop through all of the columns and rows.

rets_log = np.log(stocks / stocks.shift(1))  
rets_log

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2010-01-04	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2010-01-05	0.001727	0.000323	-0.000479	0.005883	0.017525	0.002644	0.003111	-0.035038	-0.002988	-0.001206	0.009595	-0.000911
2010-01-06	-0.016034	-0.006156	-0.003360	-0.018282	-0.010731	0.000704	0.000545	-0.009868	0.003058	0.017589	0.023999	0.016365
2010-01-07	-0.001850	-0.010389	-0.009662	-0.017160	0.019379	0.004212	0.003993	-0.005233	-0.006544	-0.005814	-0.004876	-0.006207
2010-01-08	0.006626	0.006807	0.011103	0.026717	-0.019093	0.003322	0.002878	-0.050024	0.006544	0.003704	0.014959	0.004951
...	...	...	...	...	...	...	...	...	...	...	...	...
2018-06-25	-0.014983	-0.020323	-0.034690	-0.031090	-0.020020	-0.013706	-0.013820	0.229947	0.004024	-0.002755	-0.007694	-0.003746
2018-06-26	0.012330	0.006988	-0.020722	0.016660	0.000181	0.002212	0.002202	-0.084863	-0.004883	-0.005040	-0.002730	-0.005269
2018-06-27	-0.001465	-0.015665	-0.018491	-0.018249	-0.006338	-0.008319	-0.008642	0.117783	-0.008018	-0.005593	-0.006399	-0.005718
2018-06-28	0.007250	0.011113	0.009999	0.024356	0.014608	0.005701	0.006160	-0.061009	0.001298	-0.002993	0.005487	-0.003041
2018-06-29	-0.002105	-0.000203	0.009297	-0.000970	-0.012838	0.001439	0.000758	-0.046153	0.009979	0.003496	0.017179	0.003631

2138 rows × 12 columns

We can then use the fact that you can sum up log returns over time to get cumulative, or total log returns. First, you can use the .cumsum() function from pandas to transform our daily returns into a cumulative sum. In other words, each period is now the sum of all returns in the previous periods.

rets_log.cumsum()

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2010-01-04	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2010-01-05	0.001727	0.000323	-0.000479	0.005883	0.017525	0.002644	0.003111	-0.035038	-0.002988	-0.001206	0.009595	-0.000911
2010-01-06	-0.014307	-0.005833	-0.003839	-0.012399	0.006795	0.003347	0.003656	-0.044906	0.000069	0.016383	0.033594	0.015454
2010-01-07	-0.016157	-0.016221	-0.013501	-0.029559	0.026174	0.007560	0.007649	-0.050138	-0.006474	0.010569	0.028718	0.009247
2010-01-08	-0.009531	-0.009414	-0.002398	-0.002842	0.007081	0.010882	0.010527	-0.100162	0.000069	0.014273	0.043677	0.014197
...	...	...	...	...	...	...	...	...	...	...	...	...
2018-06-25	1.784829	1.156566	0.887331	2.519375	0.246849	0.871815	0.874694	-0.145291	-0.208232	0.121743	-0.773644	0.087914
2018-06-26	1.797158	1.163555	0.866609	2.536035	0.247030	0.874026	0.876896	-0.230154	-0.213115	0.116703	-0.776374	0.082645
2018-06-27	1.795693	1.147890	0.848119	2.517787	0.240691	0.865708	0.868255	-0.112371	-0.221133	0.111110	-0.782772	0.076927
2018-06-28	1.802943	1.159002	0.858118	2.542143	0.255299	0.871409	0.874414	-0.173380	-0.219836	0.108117	-0.777285	0.073887
2018-06-29	1.800839	1.158800	0.867414	2.541173	0.242461	0.872848	0.875172	-0.219532	-0.209857	0.111613	-0.760106	0.077517

2138 rows × 12 columns

If you take the cumulative sum of log returns (R) at any point and do e^R, then you get the value of $1 invested at the beginning. We can use .apply() to “apply” the exponential function e to each value in the DataFrame. If you want to convert back to the cumulative simple return instead, you can do e^R - 1.

rets_log.cumsum().apply(np.exp)

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2010-01-04	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2010-01-05	1.001729	1.000323	0.999521	1.005900	1.017680	1.002647	1.003116	0.965569	0.997016	0.998795	1.009642	0.999089
2010-01-06	0.985795	0.994184	0.996169	0.987677	1.006818	1.003353	1.003663	0.956088	1.000069	1.016518	1.034165	1.015574
2010-01-07	0.983973	0.983910	0.986590	0.970874	1.026520	1.007588	1.007679	0.951098	0.993547	1.010625	1.029134	1.009290
2010-01-08	0.990514	0.990630	0.997605	0.997162	1.007107	1.010941	1.010583	0.904691	1.000069	1.014375	1.044645	1.014299
...	...	...	...	...	...	...	...	...	...	...	...	...
2018-06-25	5.958559	3.178998	2.428640	12.420836	1.279986	2.391247	2.398141	0.864770	0.812019	1.129464	0.461329	1.091894
2018-06-26	6.032481	3.201292	2.378831	12.629500	1.280217	2.396541	2.403428	0.794411	0.808063	1.123786	0.460071	1.086157
2018-06-27	6.023650	3.151535	2.335249	12.401120	1.272128	2.376688	2.382748	0.893713	0.801610	1.117518	0.457137	1.079964
2018-06-28	6.067480	3.186753	2.358716	12.706871	1.290848	2.390276	2.397470	0.840818	0.802651	1.114179	0.459652	1.076685
2018-06-29	6.054723	3.186107	2.380747	12.694548	1.274382	2.393717	2.399289	0.802894	0.810700	1.118080	0.467617	1.080601

2138 rows × 12 columns

print(np.exp(1.800839))

6.054725248468137

You can then plot the cumulative returns. Notice how we use the . to keep sending the DataFrame through to the next step. Take the raw data, do something to it, do something else to that result, and then plot it.

rets_log.cumsum().apply(np.exp).plot(figsize=(10, 6));  

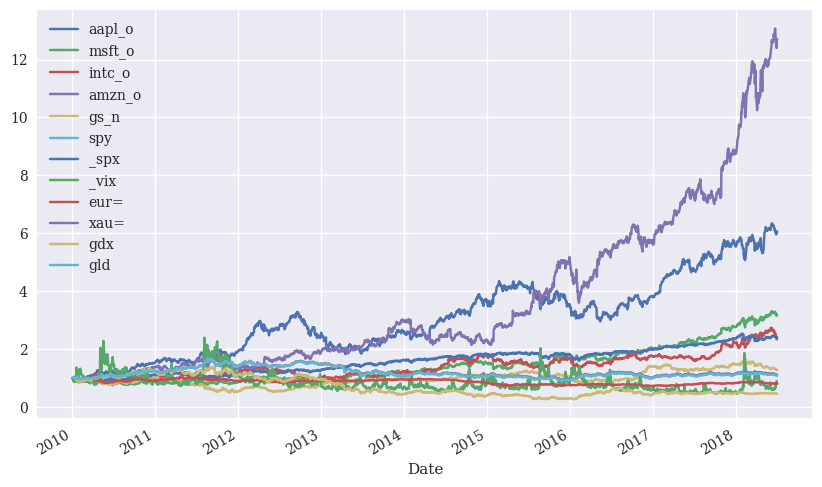
We can also create return series using simple returns. We calculate percent returns, add 1 to each to get (1+R), and then chain returns together using .cumprod(). We subtract one at the end from the total.

In other words,

(7.3)\[\begin{align} Total Return = (1 + R_{1})*(1 + R_{2})*(1 + R_{3})*(1 + R_{4})... - 1 \end{align}\]

rets_simple = stocks.pct_change() # period return
rets_simple = rets_simple.add(1)
rets_simple.head()

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2010-01-04	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2010-01-05	1.001729	1.000323	0.999521	1.005900	1.017680	1.002647	1.003116	0.965569	0.997016	0.998795	1.009642	0.999089
2010-01-06	0.984094	0.993863	0.996646	0.981884	0.989327	1.000704	1.000546	0.990181	1.003062	1.017745	1.024289	1.016500
2010-01-07	0.998151	0.989665	0.990385	0.982987	1.019568	1.004221	1.004001	0.994781	0.993478	0.994203	0.995136	0.993812
2010-01-08	1.006648	1.006830	1.011165	1.027077	0.981089	1.003328	1.002882	0.951207	1.006565	1.003711	1.015071	1.004963

rets_simple_cumulative = rets_simple.cumprod().sub(1)
rets_simple_cumulative

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2010-01-04	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2010-01-05	0.001729	0.000323	-0.000479	0.005900	0.017680	0.002647	0.003116	-0.034431	-0.002984	-0.001205	0.009642	-0.000911
2010-01-06	-0.014205	-0.005816	-0.003831	-0.012323	0.006818	0.003353	0.003663	-0.043912	0.000069	0.016518	0.034165	0.015574
2010-01-07	-0.016027	-0.016090	-0.013410	-0.029126	0.026520	0.007588	0.007679	-0.048902	-0.006453	0.010625	0.029134	0.009290
2010-01-08	-0.009486	-0.009370	-0.002395	-0.002838	0.007107	0.010941	0.010583	-0.095309	0.000069	0.014375	0.044645	0.014299
...	...	...	...	...	...	...	...	...	...	...	...	...
2018-06-25	4.958559	2.178998	1.428640	11.420836	0.279986	1.391247	1.398141	-0.135230	-0.187981	0.129464	-0.538671	0.091894
2018-06-26	5.032481	2.201292	1.378831	11.629500	0.280217	1.396541	1.403428	-0.205589	-0.191937	0.123786	-0.539929	0.086157
2018-06-27	5.023650	2.151535	1.335249	11.401120	0.272128	1.376688	1.382748	-0.106287	-0.198390	0.117518	-0.542863	0.079964
2018-06-28	5.067480	2.186753	1.358716	11.706871	0.290848	1.390276	1.397470	-0.159182	-0.197349	0.114179	-0.540348	0.076685
2018-06-29	5.054723	2.186107	1.380747	11.694548	0.274382	1.393717	1.399289	-0.197106	-0.189300	0.118080	-0.532383	0.080601

2138 rows × 12 columns

7.3. Normalizing price series

You often see charts where all of the assets start at a price of 1 or 100. You can then compare their growth over time. We can easily do this using pandas.

We can divide all of the prices by the first price in the series, creating prices relative to that starting point.

We can pull the first price for one stock using .iloc.

stocks.aapl_o.iloc[0]

30.57282657

We can also pull all of the first prices.

stocks.iloc[0]

aapl_o      30.572827
msft_o      30.950000
intc_o      20.880000
amzn_o     133.900000
gs_n       173.080000
spy        113.330000
_spx      1132.990000
_vix        20.040000
eur=         1.441100
xau=      1120.000000
gdx         47.710000
gld        109.800000
Name: 2010-01-04 00:00:00, dtype: float64

We can use .div() to divide every item in a column by the first item in that column. This is yet another example of vectorization making our lives easier. As the DataCamp assignment notes, .div() and other math functions automatically align series and DataFrame columns. So, each price in the first column gets divided by the first price in the first column, etc.

normalized = stocks.div(stocks.iloc[0]).mul(100)
normalized.plot()

<AxesSubplot:xlabel='Date'>

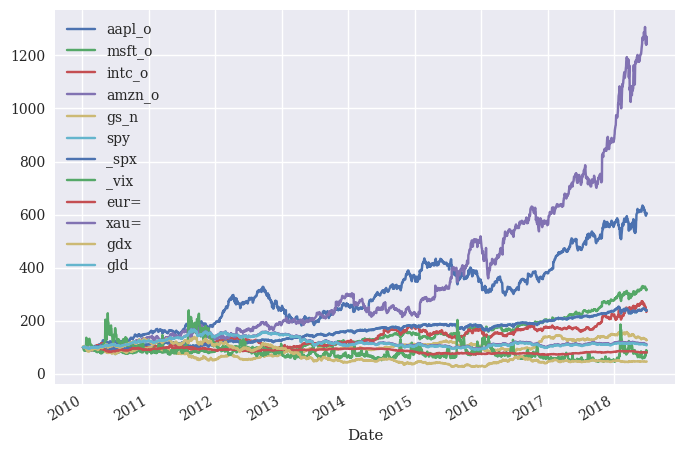
7.4. Resampling

Resampling is when you change the time period that you’re looking at. So, you can go from daily to weekly to monthly, etc. This is called downsampling and involves aggregating your data.

You can also do the opposite and go from, say, monthly to daily. The new dates created in your data will be set as NaN. This is called upsampling and involves filling in missing data.

Let’s start with .asfreq and some basic fill methods. I am going to “create” some quarterly data first for us to work with. I’ll discuss how I do this in a minute.

stocks_quarterly = stocks.resample('1q', label='right').last()
stocks_quarterly.head()

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2010-03-31	33.571395	29.2875	22.29	135.77	170.63	117.00	1169.43	17.59	1.3510	1112.80	44.41	108.95
2010-06-30	35.932821	23.0100	19.45	109.26	131.27	103.22	1030.71	34.54	1.2234	1241.35	51.96	121.68
2010-09-30	40.535674	24.4900	19.20	157.06	144.58	114.13	1141.20	23.70	1.3630	1308.50	55.93	127.91
2010-12-31	46.079954	27.9100	21.03	180.00	168.16	125.75	1257.64	17.75	1.3377	1419.45	61.47	138.72
2011-03-31	49.786736	25.3900	20.18	180.13	158.47	132.59	1325.83	17.74	1.4165	1430.00	60.10	139.86

Alright, we have some quarterly stock price data now. But, what I want to make this monthly data? Well, I don’t have the actual monthly prices in this data set, but I can still upsample the data and go from quarterly to monthly.

stocks_monthly = stocks_quarterly.asfreq('M')
stocks_monthly.head()

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2010-03-31	33.571395	29.2875	22.29	135.77	170.63	117.00	1169.43	17.59	1.3510	1112.80	44.41	108.95
2010-04-30	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2010-05-31	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
2010-06-30	35.932821	23.0100	19.45	109.26	131.27	103.22	1030.71	34.54	1.2234	1241.35	51.96	121.68
2010-07-31	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN

We now have new dates and missing values. We could fill in these missing values like we want. `.asfreq()’ has different methods. I’ll fill with the previous value, so that April and May get a March value, etc. This is called a forward fill.

stocks_monthly = stocks_quarterly.asfreq('M', method='ffill')
stocks_monthly.head()

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2010-03-31	33.571395	29.2875	22.29	135.77	170.63	117.00	1169.43	17.59	1.3510	1112.80	44.41	108.95
2010-04-30	33.571395	29.2875	22.29	135.77	170.63	117.00	1169.43	17.59	1.3510	1112.80	44.41	108.95
2010-05-31	33.571395	29.2875	22.29	135.77	170.63	117.00	1169.43	17.59	1.3510	1112.80	44.41	108.95
2010-06-30	35.932821	23.0100	19.45	109.26	131.27	103.22	1030.71	34.54	1.2234	1241.35	51.96	121.68
2010-07-31	35.932821	23.0100	19.45	109.26	131.27	103.22	1030.71	34.54	1.2234	1241.35	51.96	121.68

pandas also has a method called .resample. This is a lot like a .groupby(), but dealing with time.

The code stocks.resample('1w', label='right') creates what pandas calls a DatetimeIndexResampler object. Basically, we are creating “bins” based on the time period we specify. I start with one week and then do one month. The argument label='right' tells .resample() which bin edge to label the bucket with. So, the first edge (i.e. the first date) or the last edge (i.e. the last date). The option right means the last edge. For example, the bin will get labeled with the last day of the week. Or the last day of the month. The method .last() picks the last member of each time bin. So, we’ll get get end-of-week prices or end-of-month prices.

You can find the documentation here. The fourth DataCamp assignment also goes over the details.

stocks.resample('1w', label='right').last().head()  

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2010-01-10	30.282827	30.66	20.83	133.52	174.31	114.57	1144.98	18.13	1.4412	1136.10	49.84	111.37
2010-01-17	29.418542	30.86	20.80	127.14	165.21	113.64	1136.03	17.91	1.4382	1129.90	47.42	110.86
2010-01-24	28.249972	28.96	19.91	121.43	154.12	109.21	1091.76	27.31	1.4137	1092.60	43.79	107.17
2010-01-31	27.437544	28.18	19.40	125.41	148.72	107.39	1073.87	24.62	1.3862	1081.05	40.72	105.96
2010-02-07	27.922829	28.02	19.47	117.39	154.16	106.66	1066.19	26.11	1.3662	1064.95	42.41	104.68

stocks.resample('1m', label='right').last().head()  

	aapl_o	msft_o	intc_o	amzn_o	gs_n	spy	_spx	_vix	eur=	xau=	gdx	gld
Date
2010-01-31	27.437544	28.1800	19.40	125.41	148.72	107.3900	1073.87	24.62	1.3862	1081.05	40.72	105.960
2010-02-28	29.231399	28.6700	20.53	118.40	156.35	110.7400	1104.49	19.50	1.3625	1116.10	43.89	109.430
2010-03-31	33.571395	29.2875	22.29	135.77	170.63	117.0000	1169.43	17.59	1.3510	1112.80	44.41	108.950
2010-04-30	37.298534	30.5350	22.84	137.10	145.20	118.8125	1186.69	22.05	1.3295	1178.25	50.51	115.360
2010-05-31	36.697106	25.8000	21.42	125.46	144.26	109.3690	1089.41	32.07	1.2267	1213.81	49.86	118.881

rets_log.cumsum().apply(np.exp).resample('1m', label='right').last(
                          ).plot(figsize=(10, 6));  

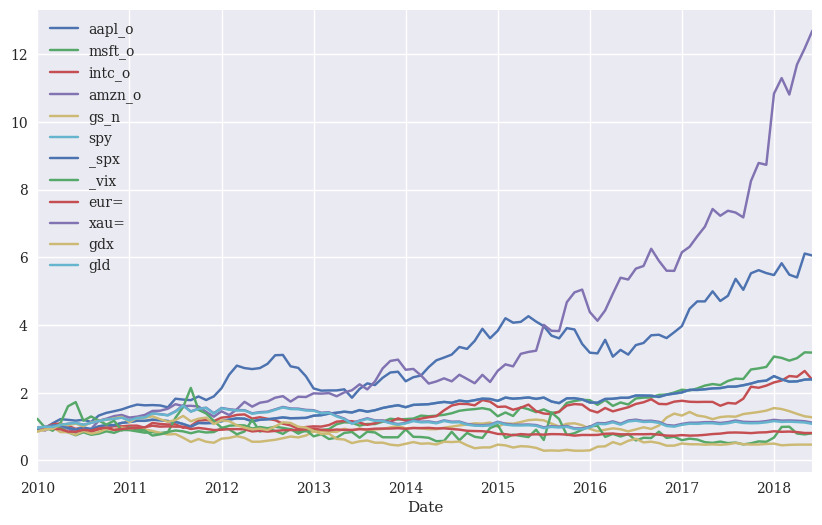
7.5. Rolling statistics

Rolling statistics are your usual sorts of statistics, like a mean or standard deviation, but calculated with rolling time windows. So, the average price over the past month. Or, the standard deviation of returns of the past year. The value gets updated as you move forward in time - this is the rolling part.

Let’s set a 20 day window and calculate some rolling statistics. There’s one you might not know, a kind of moving average called an exponentially weighted moving average (ewma).

window = 20  

stocks['aapl_min'] = stocks['aapl_o'].rolling(window=window).min()  
stocks['aapl_mean'] = stocks['aapl_o'].rolling(window=window).mean()  
stocks['aapl_std'] = stocks['aapl_o'].rolling(window=window).std()  
stocks['aapl_max'] = stocks['aapl_o'].rolling(window=window).max()  
stocks['aapl_ewma'] = stocks['aapl_o'].ewm(halflife=0.5, min_periods=window).mean()  

Let’s make a plot using pandas plot. I’ll select four variables and then pick just the last 200 observations using .iloc. Notice I don’t need to include the index value. This is a line graph, so .plot() knows that you want this on the x-axis. I like how .plot() automatically styles the x-axis for us too.

stocks[['aapl_min', 'aapl_mean', 'aapl_max', 'aapl_o']].iloc[-200:].plot(style=['g--', 'r--', 'g--', 'b'], lw=0.8, figsize=(10, 6), title = 'Apple Price with 20-Day Rolling Window Statistics');  

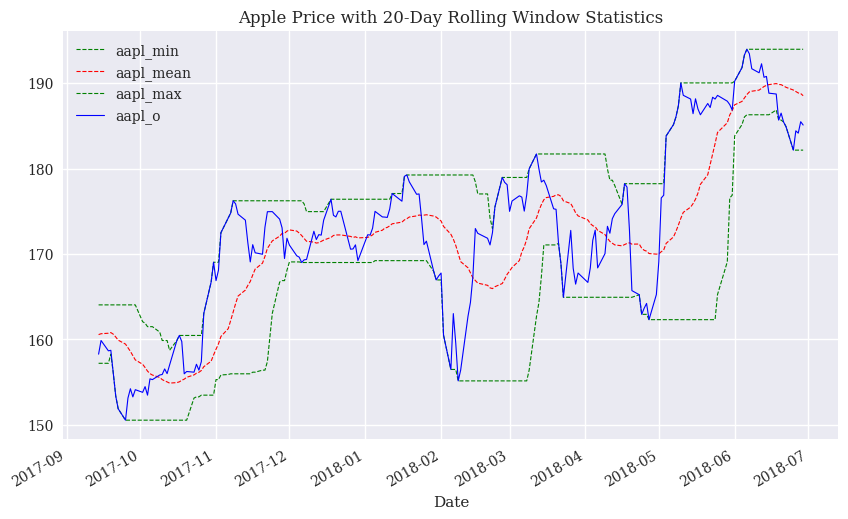
Now, I’ll make the same graph using matplotlib. Again, I don’t include the index value, as, by default, matplotlib will put it on the x-axis. I’m going to put four different line plots on the same axis. I am again selecting just the last 200 rows using .iloc().

fig = plt.figure(figsize=(10, 6))

ax = fig.add_subplot(1, 1, 1)

ax.plot(stocks.aapl_min.iloc[-200:], 'g--', lw=0.8)
ax.plot(stocks.aapl_mean.iloc[-200:], 'r--', lw=0.8)
ax.plot(stocks.aapl_max.iloc[-200:], 'g--', lw=0.8)
ax.plot(stocks.aapl_o.iloc[-200:], 'b', lw=0.8)

ax.set_xlabel('Date')
ax.set_ylabel('Apple Price')
ax.set_title('Apple Price with 20-Day Rolling Window Statistics');

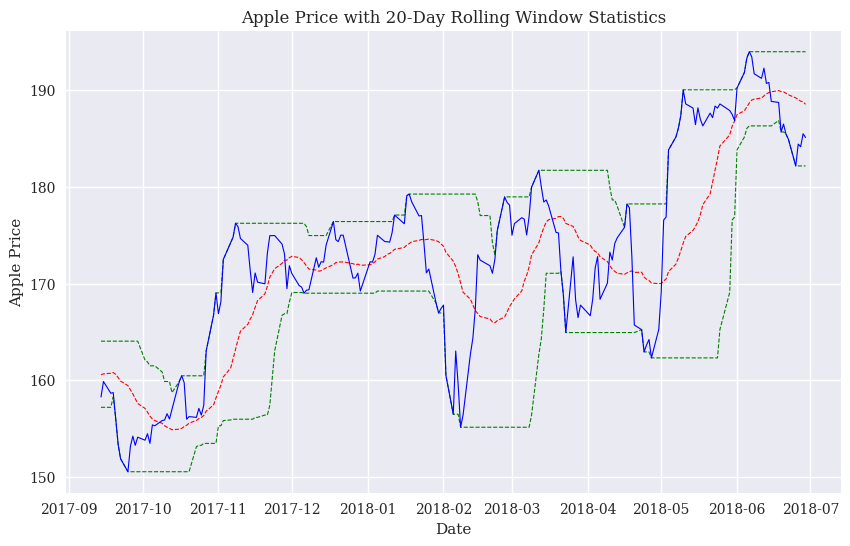
Which way should you make your plots? Basically up to you! There are less verbose ways to do it that the matplotlib method I used above. I kind of like seeing each line like that, as it helps me read and understand what’s going on.

You could also select just the data you want, save it to a new DataFrame, and then plot.

stocks_last200 = stocks.iloc[-200:]

fig = plt.figure(figsize=(10, 6))

ax = fig.add_subplot(1, 1, 1)

ax.plot(stocks_last200.aapl_min, 'g--', lw=0.8)
ax.plot(stocks_last200.aapl_mean, 'r--', lw=0.8)
ax.plot(stocks_last200.aapl_max, 'g--', lw=0.8)
ax.plot(stocks_last200.aapl_o, 'b', lw=0.8)

ax.set_xlabel('Date')
ax.set_ylabel('Apple Price')
ax.set_title('Apple Price with 20-Day Rolling Window Statistics');

7.5.1. Simple trend indicator

One of the best known “anomalies” in finance is that stocks that have been doing better perform better in the future, and vice-versa. This general set of anomalies are called momentum and trend. Here’s a summary of momentum and why it might exist. The hedge fund Two Sigma has a brief explanation of how trend and momentum are different. And a more academic explanation.

We can calculate basic moving averages that might capture the spirit of trend. We want stocks that are outperforming their longer history in the short-term. We can measure this with two different simple moving averages (sma).

stocks['aapl_sma_42'] = stocks['aapl_o'].rolling(window=42).mean()
stocks['aapl_sma_252'] = stocks['aapl_o'].rolling(window=252).mean()  

stocks[['aapl_o', 'aapl_sma_42', 'aapl_sma_252']].plot(figsize=(10, 6));  

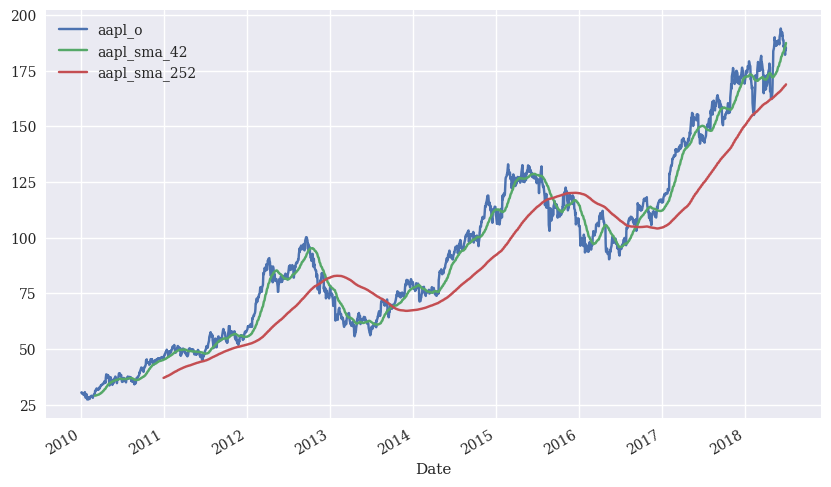
Let’s create an indicator (1/0) variable that is 1 if the two-month moving average is above the one-year moving average. This would be example of a simple short-term trend strategy. You buy the stock if it is doing better now than it has in over the past year. You do not own the stock otherwise.

I will then graph the moving averages, the price, and the indicator, called take_position, on the same graph. I’m going to do something a bit different, but you’ll see it in our text. I will use pandas .plot() to make the graph, but save this to an axes object. I can then refer to the ax object when styling. This kind of mixes two ways that we’ve seen plot and figure creation!

Notice the creation of a secondary y-axis for the indicator variable.

stocks['take_position'] = np.where(stocks['aapl_sma_42'] > stocks['aapl_sma_252'], 1, -1)  

ax = stocks[['aapl_o', 'aapl_sma_42', 'aapl_sma_252', 'take_position']].plot(figsize=(10, 6), secondary_y='take_position')
ax.get_legend().set_bbox_to_anchor((0.25, 0.85));

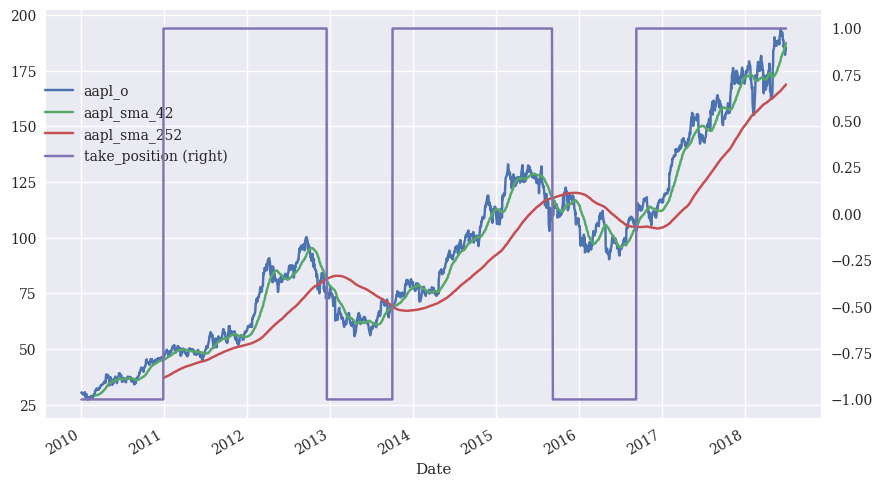
What do you think? Did this strategy work for trading Apple during the 2010s? We’ll look more at backtesting strategies and all of the issues that arise later on.

7.6. Correlation and regression

We’ll look at some simple correlation and linear regression calculations. We’ll do more with regression later on.

Let’s look at the relationship between the S&P 500 and the Apple. I’ll bring the stocks data again, but just keep these two time series. I won’t bother cleaning the names. pyjanitor replaces the . in front of .SPX with an underscore and plot() doesn’t like that when making the legend.

# Read in some eod prices
stocks2 = pd.read_csv('https://raw.githubusercontent.com/aaiken1/fin-data-analysis-python/main/data/tr_eikon_eod_data.csv',
                  index_col=0, parse_dates=True)  

stocks2.dropna(inplace=True)  

stocks2 = stocks2[['.SPX', 'AAPL.O']]

stocks2.plot(subplots=True, figsize=(10, 6));

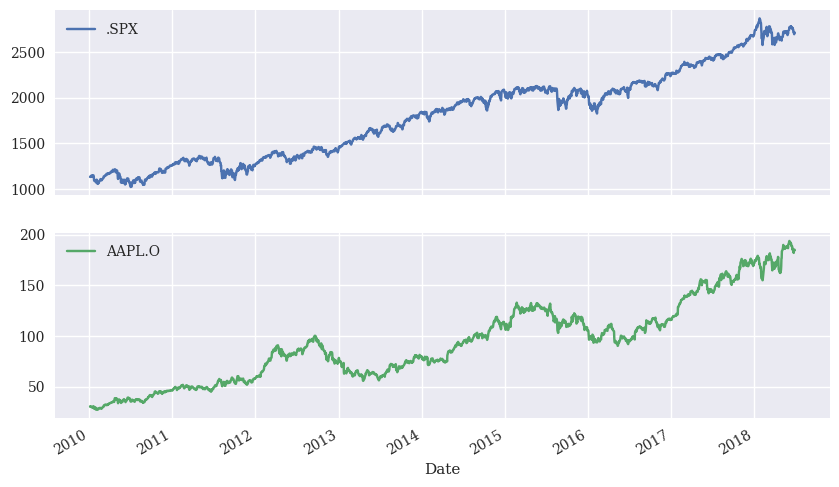
rets2 = np.log(stocks2 / stocks2.shift(1)) 

rets2.dropna(inplace=True)

pd.plotting.scatter_matrix(rets2,
                           alpha=0.2,  
                           diagonal='hist',  
                           hist_kwds={'bins': 35},  
                           figsize=(10, 6));

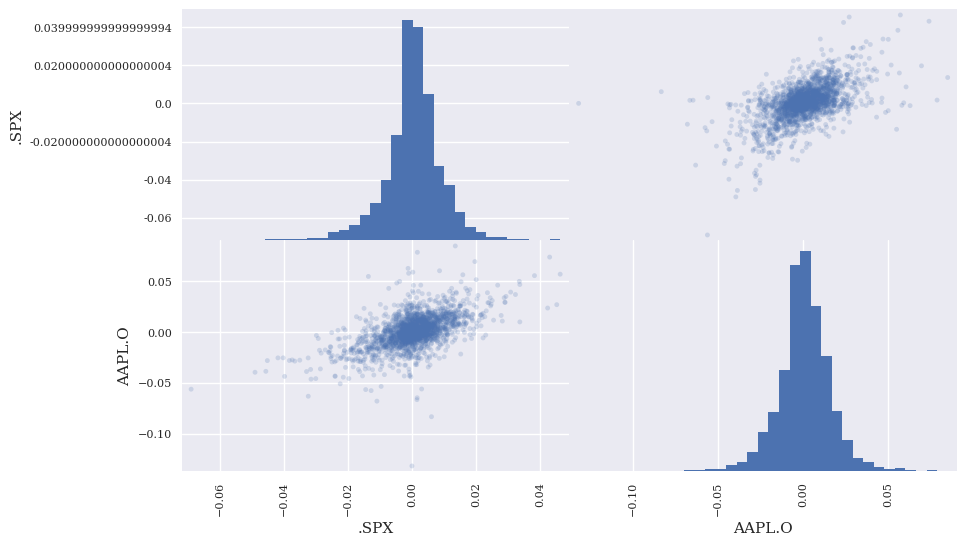
rets2

	.SPX	AAPL.O
Date
2010-01-05	0.003111	0.001727
2010-01-06	0.000545	-0.016034
2010-01-07	0.003993	-0.001850
2010-01-08	0.002878	0.006626
2010-01-11	0.001745	-0.008861
...	...	...
2018-06-25	-0.013820	-0.014983
2018-06-26	0.002202	0.012330
2018-06-27	-0.008642	-0.001465
2018-06-28	0.006160	0.007250
2018-06-29	0.000758	-0.002105

2137 rows × 2 columns

Yikes! Not sure about those y-axis labels. That’s some floating-point nonsense.

We can run a simple linear regression using np.polyfit from the numpy library. Other libraries have more sophisticated tools. We’ll set deg=1 since this is a linear regression (i.e. degree of 1).

reg = np.polyfit(rets2['.SPX'], rets2['AAPL.O'], deg=1)  
reg

array([9.57422130e-01, 4.50598662e-04])

Apple has a beta of 0.957 (note the scientific notation in the output). The intercept (or alpha) is the next number and is based on daily returns.

rets2.corr()  

	.SPX	AAPL.O
.SPX	1.000000	0.563036
AAPL.O	0.563036	1.000000

7.7. Generating random returns

We are going to look more at distributions and what are called Monte Carlo methods when we get to risk management, simulations, and option pricing. But, for now, let’s look at a simple case of generating some random returns that “look” like actual stock returns.

Let’s create 1000 random numbers from a normal distribution with a mean of 0 and a standard deviation of 0.01 (1%). This means that we “pull” these numbers out of that distribution. We can then plot them (using seaborn, for fun) and include a normal distribution that fits the distribution of random numbers.

seed(1986)
random_returns = normal(loc=0, scale=0.01, size=1000)
sns.distplot(random_returns, fit=norm, kde=False)

<AxesSubplot:>

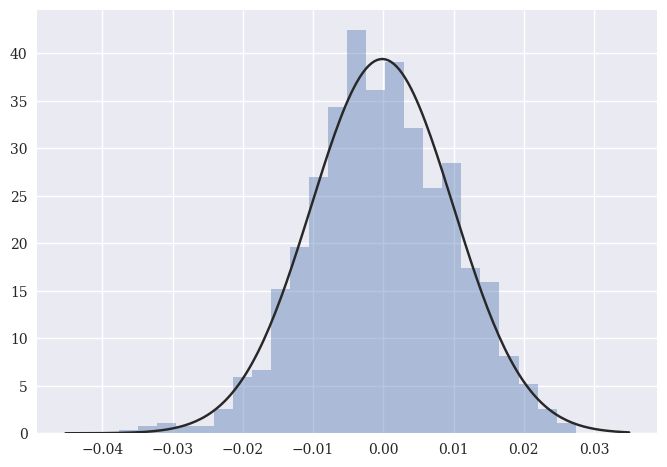
Looks like a bell curve to me. Let’s take that set of 1000 random numbers and turn them into a pd.Series. We can then treat them like actual returns and create a cumulative return series, like above.

return_series = pd.Series(random_returns)
random_prices = return_series.add(1).cumprod().sub(1)
random_prices.mul(100).plot();

And there you go! Some fake returns. Stocks returns aren’t actually normally distributed like this, at least over short windows. Simulations and Monte Carlo methods are used a lot in wealth management to figure out the probability that a client will meet their retirement goals.