Using ChatGPT
Contents
2.9. Using ChatGPT#
There are now many AI-based tools to help us code. These tools can create code outlines for us, check our own code, write functions, and explain the steps. I’m going to show you a few examples using the free OpenAI ChapGPT tools.
If you use Github and VS Code, you can sign-up for CoPilot.
This paper by Liu, Miller, and Niu (2023) has some great examples of how to use ChatGPT in a course like this one.
2.9.1. Using GPT to Write a Function For You#
Let’s go back to Chapter 7, where I showed you how to write a function to generate asset paths using geometric brownian motion. We used the Nasdaq API to bring in some bitcoin data in that example. Now, I’m going to use ChatGPT to write the same function. I gave GPT4 the following prompt:
Write a function in Python that simulates geometric brownian motion for any number of assets. Create the appropriate inputs as arrays. The inputs should be the number of assets, the mean for each asset, the standard deviation for each asset, the number of periods, the initial value of each asset, and the number of simulations. The output should be an array that contains all of the simulations for each asset. These are uncorrelated assets, so don’t worry about covariance.
Here’s the code that it gave me:
import numpy as np
def geometric_brownian_motion(num_assets, means, std_devs, num_periods, initial_values, num_simulations):
if len(means) != num_assets or len(std_devs) != num_assets or len(initial_values) != num_assets:
raise ValueError("The length of means, std_devs, and initial_values should be equal to the number of assets")
# Initialize an array to store the simulations
simulations = np.zeros((num_simulations, num_periods + 1, num_assets))
# Set the initial values for each simulation
simulations[:, 0, :] = initial_values
# Time step
dt = 1.0
# Loop through each simulation
for sim in range(num_simulations):
# Loop through each time period
for t in range(1, num_periods + 1):
# Loop through each asset
for asset in range(num_assets):
# Generate a random normal value (using mean=0 and std_dev=1) for the brownian motion
random_normal = np.random.normal(0, 1)
# Calculate the change in asset value using geometric brownian motion
change = means[asset] * dt + std_devs[asset] * np.sqrt(dt) * random_normal
# Update the asset value
simulations[sim, t, asset] = simulations[sim, t - 1, asset] * np.exp(change)
return simulations
# Example usage
num_assets = 3
means = np.array([0.05, 0.06, 0.07])
std_devs = np.array([0.1, 0.12, 0.14])
num_periods = 100
initial_values = np.array([100, 120, 140])
num_simulations = 1000
simulations = geometric_brownian_motion(num_assets, means, std_devs, num_periods, initial_values, num_simulations)
print(simulations)
[[[1.00000000e+02 1.20000000e+02 1.40000000e+02]
[1.21546818e+02 1.20903701e+02 1.58239566e+02]
[1.20339866e+02 1.18317420e+02 1.42059195e+02]
...
[5.68571150e+03 3.17746393e+04 9.05669376e+04]
[6.22339534e+03 4.26528824e+04 9.45686250e+04]
[5.54037673e+03 5.40870287e+04 9.70039992e+04]]
[[1.00000000e+02 1.20000000e+02 1.40000000e+02]
[1.15254008e+02 1.01782779e+02 1.52267880e+02]
[1.07542241e+02 1.04274682e+02 1.47643234e+02]
...
[3.58881001e+04 9.87573940e+04 3.39384889e+05]
[3.80124681e+04 9.76664634e+04 3.17792431e+05]
[3.99883874e+04 1.29696177e+05 3.83477645e+05]]
[[1.00000000e+02 1.20000000e+02 1.40000000e+02]
[9.33420895e+01 1.17850486e+02 1.41725661e+02]
[1.06799414e+02 1.10294977e+02 1.45287102e+02]
...
[1.24871337e+04 5.18258856e+04 1.60454075e+05]
[1.23154160e+04 4.30202196e+04 1.60273874e+05]
[1.33346902e+04 5.63445301e+04 1.78037310e+05]]
...
[[1.00000000e+02 1.20000000e+02 1.40000000e+02]
[8.92813137e+01 9.91111599e+01 1.28007544e+02]
[8.21209309e+01 1.09336154e+02 1.39647885e+02]
...
[4.89885202e+03 4.40398592e+03 5.67353849e+03]
[5.88833396e+03 5.66796220e+03 6.29448484e+03]
[7.29286765e+03 5.68492841e+03 5.92439496e+03]]
[[1.00000000e+02 1.20000000e+02 1.40000000e+02]
[9.78353442e+01 9.76473937e+01 1.35126994e+02]
[1.05031474e+02 1.07262851e+02 1.76581764e+02]
...
[9.36850142e+03 1.58474969e+05 5.86411787e+05]
[1.04364293e+04 2.10720899e+05 5.69139153e+05]
[1.00993344e+04 2.31777836e+05 6.02216052e+05]]
[[1.00000000e+02 1.20000000e+02 1.40000000e+02]
[1.23612021e+02 1.30713612e+02 1.54689577e+02]
[1.16383297e+02 1.41742307e+02 1.44002484e+02]
...
[9.96192036e+03 1.24895947e+04 3.25771961e+05]
[1.03952958e+04 1.55416371e+04 4.20883953e+05]
[1.14118635e+04 1.63097107e+04 6.36525386e+05]]]
Here’s the GPT explanation of the code.
This function accepts the following inputs:
num_assets: the number of assets
means: a NumPy array containing the mean return for each asset
std_devs: a NumPy array containing the standard deviation of return for each asset
num_periods: the number of time periods
initial_values: a NumPy array containing the initial value for each asset
num_simulations: the number of simulations to run
The function returns a 3D NumPy array containing the simulations for each asset, with dimensions (num_simulations, num_periods + 1, num_assets).
Let’s look a bit more at the output. I’ll get its .shape attribute.
type(simulations)
numpy.ndarray
simulations.shape
(1000, 101, 3)
The output is a three-dimensional array. We can pull out all of the simulations for one asset, as well as a single simulation for one asset. Or anything else.
# All simulations for the first asset.
simulations[:,:,0]
array([[ 100. , 121.54681837, 120.33986643, ...,
5685.71149545, 6223.39533787, 5540.37673013],
[ 100. , 115.2540076 , 107.54224134, ...,
35888.1001037 , 38012.46811347, 39988.38744126],
[ 100. , 93.34208948, 106.79941446, ...,
12487.13366941, 12315.41595695, 13334.69024023],
...,
[ 100. , 89.28131371, 82.12093092, ...,
4898.85201955, 5888.33395976, 7292.86764662],
[ 100. , 97.83534417, 105.03147425, ...,
9368.50141665, 10436.42930616, 10099.33442148],
[ 100. , 123.61202123, 116.38329738, ...,
9961.92036371, 10395.29580949, 11411.8635383 ]])
# All simulations for the second asset.
simulations[:,:,1]
array([[1.20000000e+02, 1.20903701e+02, 1.18317420e+02, ...,
3.17746393e+04, 4.26528824e+04, 5.40870287e+04],
[1.20000000e+02, 1.01782779e+02, 1.04274682e+02, ...,
9.87573940e+04, 9.76664634e+04, 1.29696177e+05],
[1.20000000e+02, 1.17850486e+02, 1.10294977e+02, ...,
5.18258856e+04, 4.30202196e+04, 5.63445301e+04],
...,
[1.20000000e+02, 9.91111599e+01, 1.09336154e+02, ...,
4.40398592e+03, 5.66796220e+03, 5.68492841e+03],
[1.20000000e+02, 9.76473937e+01, 1.07262851e+02, ...,
1.58474969e+05, 2.10720899e+05, 2.31777836e+05],
[1.20000000e+02, 1.30713612e+02, 1.41742307e+02, ...,
1.24895947e+04, 1.55416371e+04, 1.63097107e+04]])
# First simulation for the first asset
simulations[0,:,0]
array([ 100. , 121.54681837, 120.33986643, 117.85529164,
138.80035337, 151.66767551, 164.06992834, 171.75907136,
174.69224602, 177.50387678, 172.18435434, 170.56973861,
201.4964806 , 214.66932614, 240.94460649, 273.96090064,
328.34811306, 349.26319538, 384.0272036 , 331.37136415,
309.65885473, 301.41672607, 331.13169183, 384.9585797 ,
381.85026167, 428.455811 , 406.99197554, 392.69164965,
401.28286898, 360.62507874, 418.47470015, 504.84956201,
527.61827033, 550.46697431, 575.09534426, 560.08881704,
658.03214025, 658.04641412, 769.99201134, 871.70048621,
814.78906426, 945.98095113, 880.52728241, 1053.20180556,
949.9775449 , 958.69087299, 894.41644555, 1125.53894141,
1002.82972023, 890.17854123, 972.36728941, 987.99084351,
1161.08762445, 1104.58201872, 1150.33184995, 848.73321025,
878.50951385, 906.04021209, 988.48841838, 1175.94179832,
1087.91490232, 1209.36901617, 1195.08531072, 1251.98675914,
1356.74317718, 1418.41189181, 1721.54594488, 1495.43111539,
1374.81163493, 1488.02985638, 1485.9112785 , 1692.90764265,
1497.74146671, 1772.45497985, 1614.36021343, 1535.59883759,
1438.51630732, 1535.85606335, 1521.89057291, 1666.97791998,
1732.78786746, 1756.50923769, 1974.14425378, 2280.06103389,
2616.71789812, 3131.80417821, 2816.98246691, 3319.47636237,
3654.85410701, 3466.54996158, 3764.46040128, 3726.43872565,
4267.83928824, 4264.92776657, 4478.644554 , 4206.37939838,
4723.92492887, 5135.95853396, 5685.71149545, 6223.39533787,
5540.37673013])
Compare this code to the one we used above. What’s different? What stands out to you? What assumptions did it make? What’s up with these numbers?
GPT is quite good at creating code that has been done in a lot of places. It has trained on millions of online tutorials and examples. However, you still want to follow the logic and check for errors. There will be errors.
You can have a “dialog” with GPT. Look at the code. Is it what you want? You can ask it to change it for you.
What does that leave for us to do? Use GPT to start sketching your code, do to certain tasks. Figure out what you need. Figure out the questions that you’re trying answer. What’s the problem that you’re trying to solve? Who are you solving it for? What will the answer look like? What will it tell you?
Using tools like GPT, Github Co-Pilot, etc. is like having a team of junior programmers working for you. They can make the job easier, but it is still up to you to know what’s an interesting question in the first place. You still need to use your domain expertise and creativity to come up with solutions to problems that aren’t in an online Python tutorials.
2.9.2. Using ChatGPT to Check Our Code#
Below, I have borrowed some code from our portfolio optimization code. However, there is one small problem, based on one I encountered in class. One of those small, tiny errors that can be so frustrating! Do you see it?
# Read in some eod prices
import numpy as np
import pandas as pd
from pylab import mpl, plt
import scipy.optimize as sco
raw = pd.read_csv('https://raw.githubusercontent.com/aaiken1/fin-data-analysis-python/main/data/tr_eikon_eod_data.csv',
index_col=0, parse_dates=True).dropna()
symbols = ['AAPL.O', 'MSFT.O', 'SPY', 'GLD'] #two stocks and two ETFs
noa = len(symbols) #noa = number of assets
data = raw[symbols]
rets = data.pct_change().dropna()
noa = 4
weights = np.random.random(noa)
weights /= np.sum(weights)
ann_rets = rets.mean() * 252
def port_ret(weights):
return np.sum(ann_rets * weights)
def port_vol(weights):
return np.sort(np.dot(weights.T, np.dot(rets.cov() * 252, weights)))
def sharpe(weights):
return port_ret(weights) / port_vol(weights)
sharpe(weights)
---------------------------------------------------------------------------
AxisError Traceback (most recent call last)
Input In [7], in <cell line: 36>()
33 def sharpe(weights):
34 return port_ret(weights) / port_vol(weights)
---> 36 sharpe(weights)
Input In [7], in sharpe(weights)
33 def sharpe(weights):
---> 34 return port_ret(weights) / port_vol(weights)
Input In [7], in port_vol(weights)
30 def port_vol(weights):
---> 31 return np.sort(np.dot(weights.T, np.dot(rets.cov() * 252, weights)))
File <__array_function__ internals>:180, in sort(*args, **kwargs)
File /opt/anaconda3/lib/python3.9/site-packages/numpy/core/fromnumeric.py:1004, in sort(a, axis, kind, order)
1002 else:
1003 a = asanyarray(a).copy(order="K")
-> 1004 a.sort(axis=axis, kind=kind, order=order)
1005 return a
AxisError: axis -1 is out of bounds for array of dimension 0
Huh… Let’s see if ChatGPT can help us out. I’m going to copy and paste the code and ask it to find the mistake. It does!
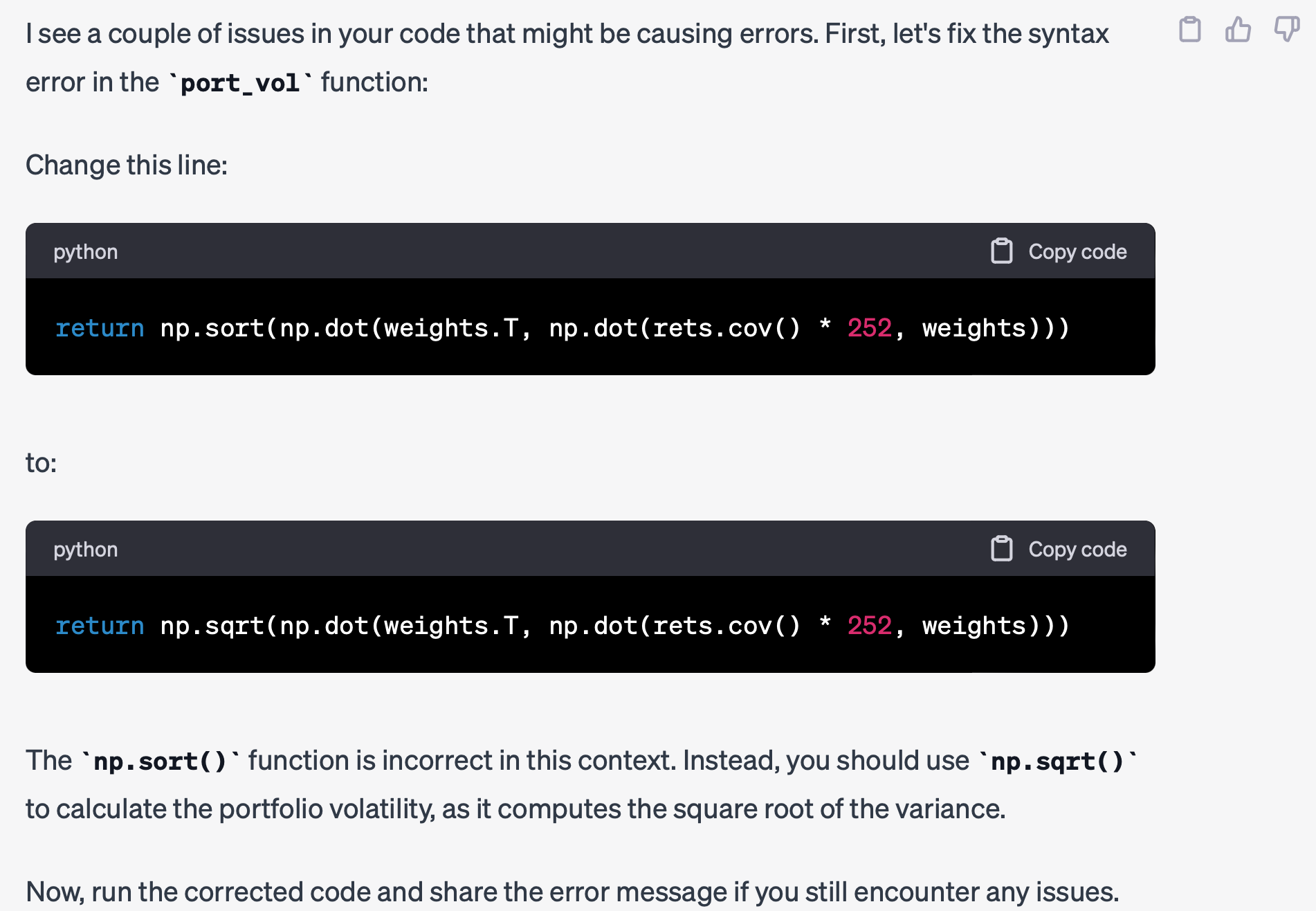
Fig. 2.26 You can use ChatGPT to find errors in your code.#

